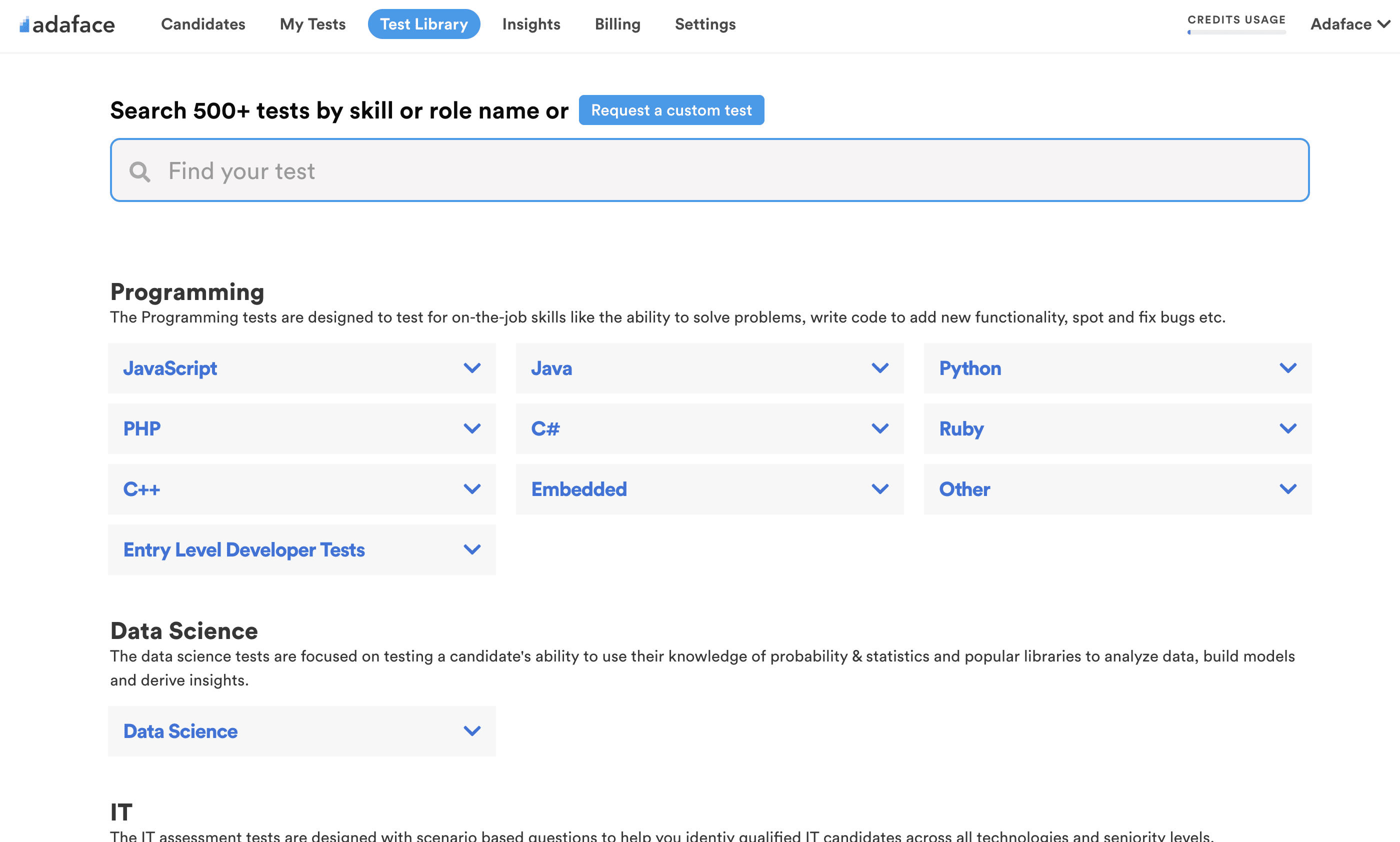
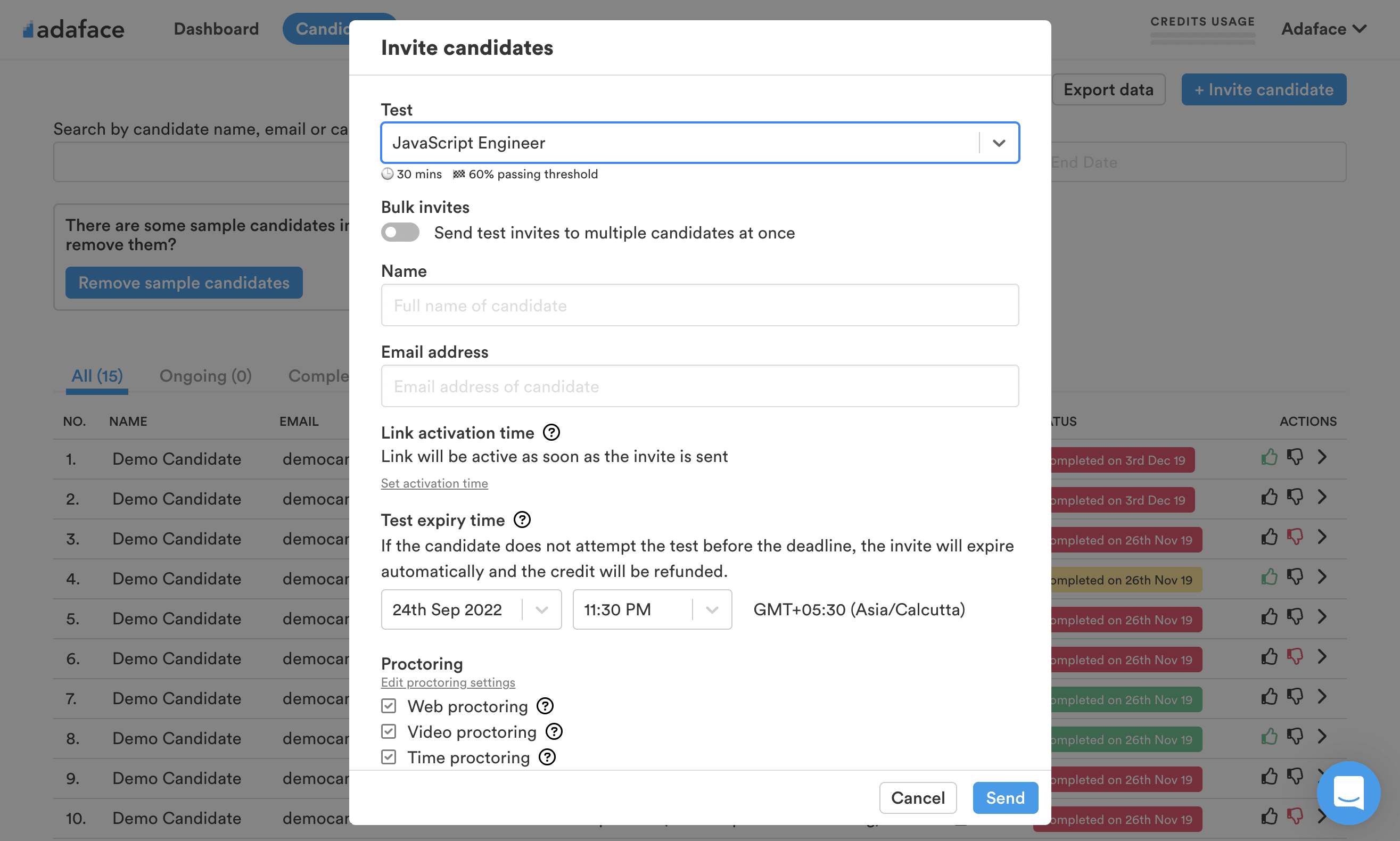
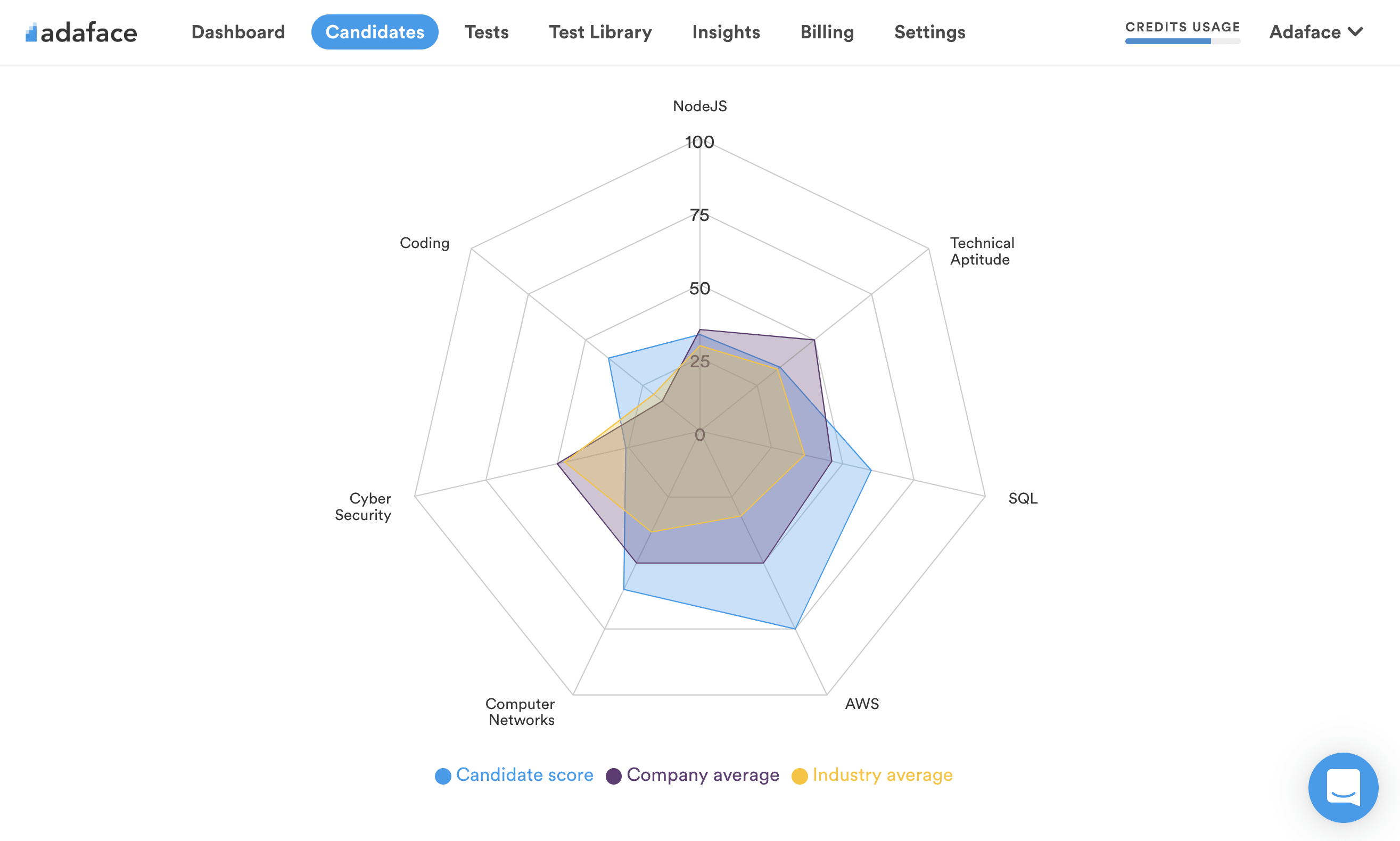
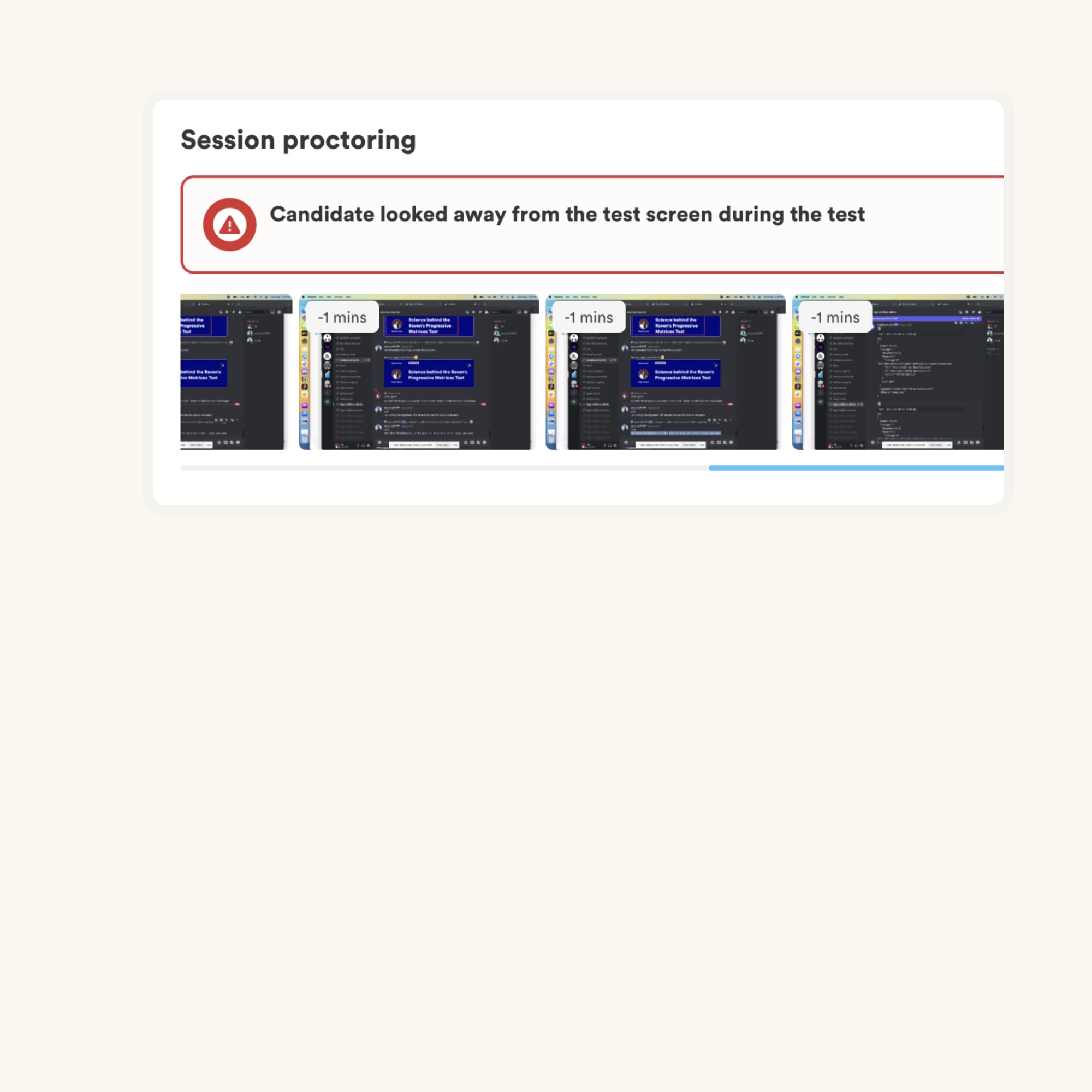
Data Structures: Data structures are fundamental constructs used to organize and store data efficiently. They include arrays, linked lists, stacks, queues, trees, and graphs. Proficiency in data structures is crucial for optimizing algorithm performance and solving complex computational problems.
Sorting and Searching Algorithms: These algorithms are essential for organizing and retrieving data efficiently. Sorting algorithms arrange data in a specific order, while searching algorithms locate specific items within a dataset. Understanding these algorithms is vital for optimizing data processing and retrieval operations.
Recursion and Backtracking: Recursion involves a function calling itself to solve smaller instances of a problem. Backtracking is a technique that explores all potential solutions by incrementally building candidates and abandoning those that fail to meet the problem's constraints. These concepts are powerful tools for solving complex problems and are often used in combinatorial optimization.
Dynamic Programming: Dynamic programming is an algorithmic paradigm that solves complex problems by breaking them down into simpler subproblems. It involves storing the results of overlapping subproblems to avoid redundant computations. This technique is crucial for optimizing algorithms and solving problems with optimal substructure.
Graph Algorithms: Graph algorithms are used to solve problems related to graph structures, such as finding shortest paths, detecting cycles, or determining connectivity. These algorithms are essential in various applications, including social network analysis, route planning, and network flow optimization.
String Manipulation: String manipulation involves operations on text data, such as searching, parsing, and modifying strings. Proficiency in string algorithms is crucial for text processing, pattern matching, and developing efficient solutions for string-related problems.
Bit Manipulation: Bit manipulation involves performing operations on individual bits or groups of bits within binary representations of data. These techniques are used for optimizing memory usage, implementing low-level system operations, and solving certain algorithmic problems more efficiently.
Mathematical Algorithms: Mathematical algorithms apply mathematical concepts to solve computational problems. They include algorithms for number theory, combinatorics, and numerical analysis. These algorithms are essential for cryptography, optimization, and scientific computing.
Tree and Binary Search Tree Algorithms: Tree algorithms operate on hierarchical data structures, while Binary Search Tree (BST) algorithms focus on efficient searching and sorting operations. These algorithms are fundamental for implementing efficient data storage and retrieval systems, as well as solving problems involving hierarchical relationships.
Hashing: Hashing is a technique used to map data of arbitrary size to fixed-size values. It is crucial for implementing efficient data structures like hash tables and solving problems that require quick lookup or data integrity verification. Understanding hashing algorithms is essential for developing scalable and performant software systems.
Complexity Analysis: Complexity analysis involves evaluating the efficiency of algorithms in terms of time and space requirements. It helps in comparing algorithms, predicting performance, and making informed decisions about algorithm selection. This skill is critical for developing scalable and efficient software solutions.
Greedy Algorithms: Greedy algorithms make locally optimal choices at each step to find a global optimum. They are used to solve optimization problems efficiently, often providing approximate solutions to NP-hard problems. Understanding greedy algorithms is crucial for developing heuristic solutions to complex problems in various domains.