Test Duration
~ 40 minsDifficulty Level
Moderate
Questions
- 2 Coding Questions
Availability
Available as custom testThe Coding: Entry-Level Algorithms Test evaluates a candidate's understanding and proficiency in fundamental algorithms and data structures. Through scenario-based MCQs and coding questions, it assesses the ability to solve problems using concepts such as sorting, searching, recursion, and more. Ideal for roles that require basic programming skills and algorithmic knowledge.
Covered skills:
Test Duration
~ 40 minsDifficulty Level
Moderate
Questions
Availability
Available as custom testThe Coding: Entry-Level Algorithms Test helps recruiters identify candidates with a solid grasp of algorithms and data structures, skills that are cornerstones of effective software development. This test helps in streamlining the hiring process by providing an objective measure of a candidate's problem-solving abilities and coding aptitude, saving valuable time and resources.
This test evaluates a candidate's proficiency in key areas like basic data structures, sorting and searching, recursion, arrays and strings, linked lists, stacks and queues, hash tables, binary trees, graphs, dynamic programming, bit manipulation, and string manipulation. It assesses their ability to apply these concepts to solve common coding challenges, demonstrating their readiness to tackle real-world problems.
Use Adaface tests trusted by recruitment teams globally. Adaface skill assessments measure on-the-job skills of candidates, providing employers with an accurate tool for screening potential hires.
We have a very high focus on the quality of questions that test for on-the-job skills. Every question is non-googleable and we have a very high bar for the level of subject matter experts we onboard to create these questions. We have crawlers to check if any of the questions are leaked online. If/ when a question gets leaked, we get an alert. We change the question for you & let you know.
How we design questionsWith Adaface, we were able to optimise our initial screening process by upwards of 75%, freeing up precious time for both hiring managers and our talent acquisition team alike!
Brandon Lee, Head of People, Love, Bonito
It's very easy to share assessments with candidates and for candidates to use. We get good feedback from candidates about completing the tests. Adaface are very responsive and friendly to deal with.
Kirsty Wood, Human Resources, WillyWeather
We were able to close 106 positions in a record time of 45 days! Adaface enables us to conduct aptitude and psychometric assessments seamlessly. My hiring managers have never been happier with the quality of candidates shortlisted.
Amit Kataria, CHRO, Hanu
We evaluated several of their competitors and found Adaface to be the most compelling. Great library of questions that are designed to test for fit rather than memorization of algorithms.
Swayam Narain, CTO, Affable
The Adaface test library features 500+ tests to enable you to test candidates on all popular skills- everything from programming languages, software frameworks, devops, logical reasoning, abstract reasoning, critical thinking, fluid intelligence, content marketing, talent acquisition, customer service, accounting, product management, sales and more.
The Coding: Entry-Level Algorithms Test is designed to assess candidates' proficiency in basic algorithm concepts. It's used by recruiters to find entry-level developers with foundational skills in algorithms and data structures, problem-solving techniques, and code efficiency.
Yes, recruiters can request a custom test that includes JavaScript questions. You can check out the JavaScript Online Test for more details on assessing JavaScript skills.
This test covers topics such as basic algorithm concepts, time complexity analysis, array and string manipulation, sorting and searching algorithms, basic data structures, recursion, mathematical algorithms, logical operators, and conditional statements.
Use this test as a pre-screening tool early in your recruitment process. Add a link to the assessment in your job post or invite candidates directly by email.
Yes, you can test JavaScript and NodeJS skills together. We recommend using the JavaScript & NodeJS Test for a comprehensive assessment.
Our main Coding tests include:
Yes, absolutely. Custom assessments are set up based on your job description, and will include questions on all must-have skills you specify. Here's a quick guide on how you can request a custom test.
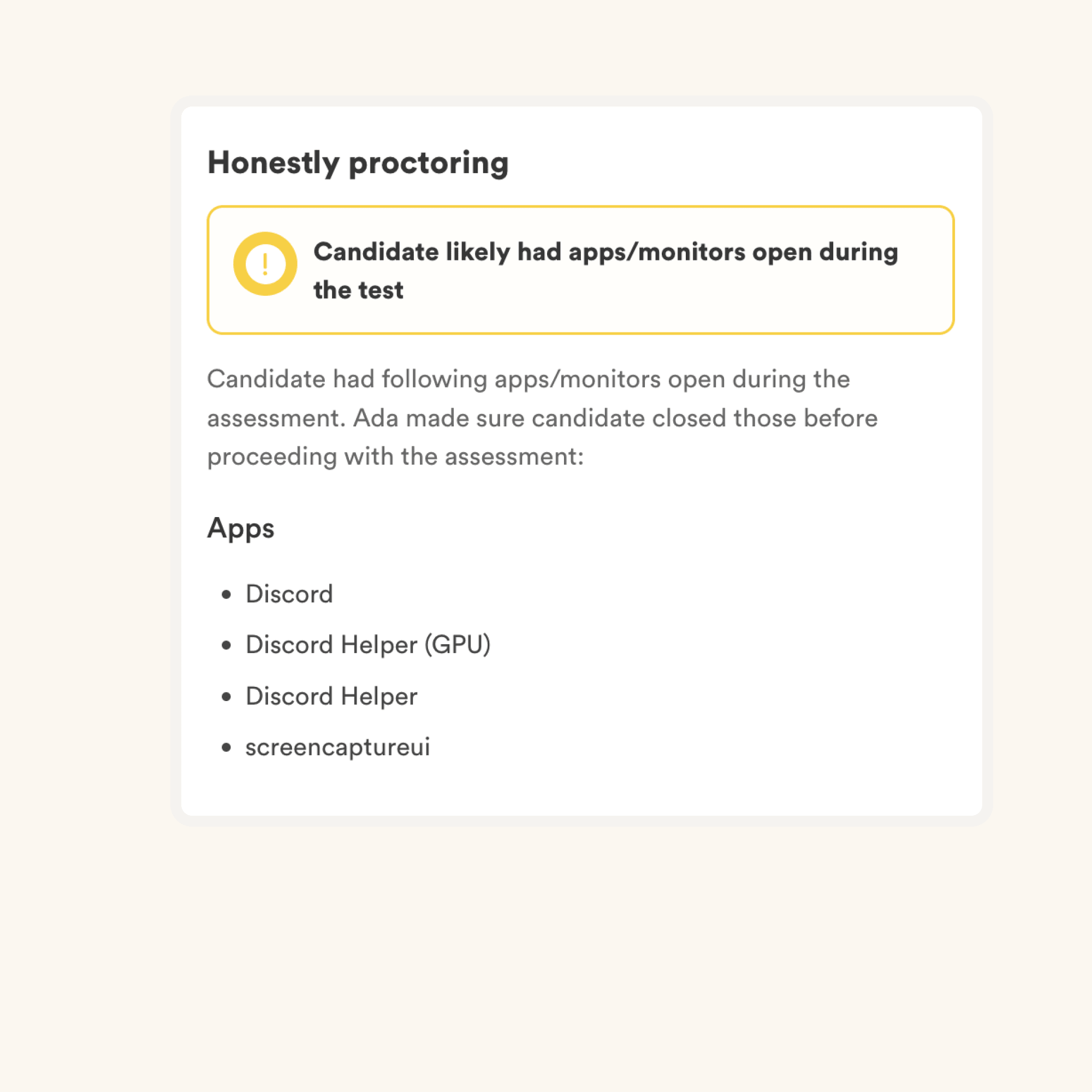
We have the following anti-cheating features in place:
Read more about the proctoring features.
The primary thing to keep in mind is that an assessment is an elimination tool, not a selection tool. A skills assessment is optimized to help you eliminate candidates who are not technically qualified for the role, it is not optimized to help you find the best candidate for the role. So the ideal way to use an assessment is to decide a threshold score (typically 55%, we help you benchmark) and invite all candidates who score above the threshold for the next rounds of interview.
Each Adaface assessment is customized to your job description/ ideal candidate persona (our subject matter experts will pick the right questions for your assessment from our library of 10000+ questions). This assessment can be customized for any experience level.
Yes, it makes it much easier for you to compare candidates. Options for MCQ questions and the order of questions are randomized. We have anti-cheating/ proctoring features in place. In our enterprise plan, we also have the option to create multiple versions of the same assessment with questions of similar difficulty levels.
No. Unfortunately, we do not support practice tests at the moment. However, you can use our sample questions for practice.
You can check out our pricing plans.
Yes, you can sign up for free and preview this test.
Here is a quick guide on how to request a custom assessment on Adaface.